알고리즘과 자료구조: 기본 개념 이해
알고리즘과 자료구조의의 기본 원리를 이해하고 간단한 문제를 해결할 수 있다.
알고리즘과 자료구조: 기본 개념 이해
📌개요
알고리즘과 자료구조의 기본 원리를 이해하고 간단한 문제를 해결할 수 있다.
📌자료구조
배열과 문자열
배열(Array)
동일한 타입의 요소들이 연속적으로 배치된 자료구조다. 인덱스를 통해 접근할 수 있으며, 고정된 크기를 갖는다.
- 장점: 인덱스를 통해 빠르게 접근 가능 (O(1))
- 단점: 크기가 고정되어 있으며, 요소의 삽입 및 삭제가 비효율적일 수 있음 (O(n))
문자열(String)
문자의 배열로, 문자열의 길이에 따라 크기가 동적으로 변할 수 있다.
- 장점: 문자열 연산(비교, 연결 등)이 간편
- 단점: 문자열의 길이에 따라 연산 시간이 증가
연결 리스트(Linked List)
각 요소가 노드로 구성되며, 각 노드는 데이터와 다음 노드를 가리키는 포인터를 포함한다. 크기가 동적으로 변한다.
- 단일 연결 리스트(Singly Linked List): 각 노드가 다음 노드를 가리킨다.
- 이중 연결 리스트(Doubly Linked List): 각 노드가 이전 노드와 다음 노드를 가리킨다.
- 장점: 크기가 동적으로 변하며, 요소의 삽입 및 삭제가 용이 (O(1))
- 단점: 인덱스를 통한 접근이 비효율적 (O(n))
스택(Stack)과 큐(Queue)
스택(Stack)
LIFO(Last In, First Out) 구조로, 마지막에 삽입된 요소가 가장 먼저 제거된다.
- 주요 연산: 삽입(push), 삭제(pop), 조회(peek)
- 장점: 구현이 간단하고, 함수 호출 스택 등에서 유용
- 단점: 특정 요소 접근이 비효율적 (O(n))
큐(Queue)
FIFO(First In, First Out) 구조로, 처음에 삽입된 요소가 가장 먼저 제거된다.
- 주요 연산: 삽입(enqueue), 삭제(dequeue), 조회(front)
- 장점: 구현이 간단하고, 작업 대기열 등에서 유용
- 단점: 특정 요소 접근이 비효율적 (O(n))
해시 테이블(Hash Table)
키-값 쌍을 저장하는 자료구조로, 해시 함수를 사용하여 키를 인덱스로 변환하여 값을 저장한다.
- 장점: 평균적으로 빠른 접근, 삽입, 삭제 가능 (O(1))
- 단점: 해시 충돌 가능성, 해시 함수의 성능에 따라 성능 차이 발생
📌알고리즘
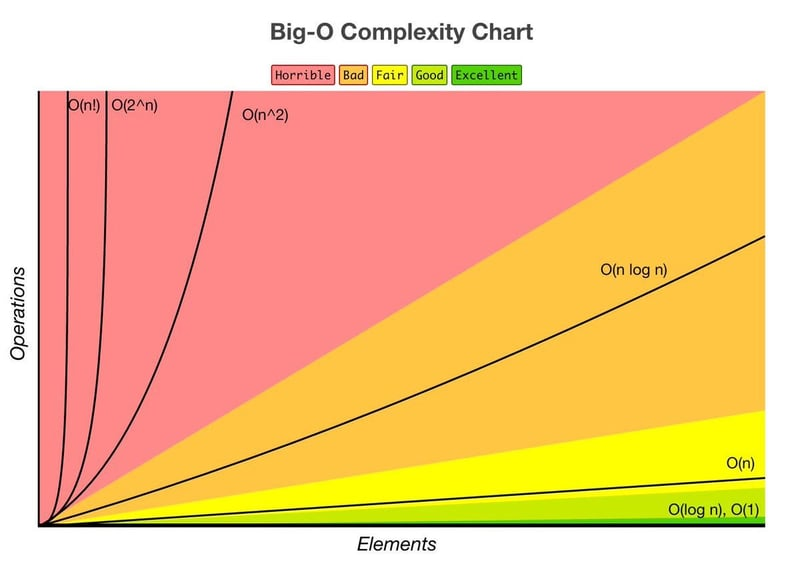
빅오 표기법(Big-O Notation)
알고리즘의 시간 복잡도와 공간 복잡도를 나타내는 표기법으로, 입력 크기 n에 대한 연산 횟수나 메모리 사용량을 표현한다.
- O(1): 상수 시간, 입력 크기에 상관없이 일정한 시간 소요
- O(n): 선형 시간, 입력 크기에 비례하여 시간 소요
- O(log n): 로그 시간, 입력 크기의 로그에 비례하여 시간 소요
- O(n^2): 이차 시간, 입력 크기의 제곱에 비례하여 시간 소요
Common Data Structure Operations
| Data Structure | Average Time Complexity | Worst Time Complexity | Worst Space Complexity | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion | ||
| Array | Θ(1) | Θ(n) | Θ(n) | Θ(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| Stack | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Queue | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Singly Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Doubly Linked List | Θ(n) | Θ(n) | Θ(1) | Θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | N/A | Θ(1) | Θ(1) | Θ(1) | N/A | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(n) | O(n) | O(n) | O(n) |
| B-Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| horrible-Black Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree | N/A | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | N/A | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| KD Tree | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | Θ(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
Array Sorting Algorithms
| Algorithm | Time Complexity | Space Complexity (Worst) | ||
|---|---|---|---|---|
| Best | Average | Worst | ||
| Quicksort | Ω(n log n) | Θ(n log n) | O(n^2) | O(log n) |
| Merge Sort | Ω(n log n) | Θ(n log n) | O(n log n) | O(n) |
| Timsort | Ω(n) | Θ(n log n) | O(n log n) | O(n) |
| Heapsort | Ω(n log n) | Θ(n log n) | O(n log n) | O(1) |
| Bubble Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Insertion Sort | Ω(n) | Θ(n^2) | O(n^2) | O(1) |
| Selection Sort | Ω(n^2) | Θ(n^2) | O(n^2) | O(1) |
| Tree Sort | Ω(n log n) | Θ(n log n) | O(n^2) | O(n) |
| Shell Sort | Ω(n log n) | Θ(n(log n)²) | O(n(log n)²) | O(1) |
| Bucket Sort | Ω(n + k) | Θ(n + k) | O(n^2) | O(n) |
| Radix Sort | Ω(nk) | Θ(nk) | O(nk) | O(n + k) |
| Counting Sort | Ω(n + k) | Θ(n + k) | O(n + k) | O(k) |
| Cubesort | Ω(n) | Θ(n log n) | O(n log n) | O(n) |
재귀(Recursion) 기본
함수가 자기 자신을 호출하는 기법으로, 문제를 작은 하위 문제로 분할하여 해결한다.
- 장점: 코드가 간결해지고, 특정 문제(예: 트리 탐색)에서 유용
- 단점: 호출 스택의 크기가 커질 수 있으며, 무한 재귀를 방지하기 위해 종료 조건 필요
정렬 알고리즘
버블 정렬(Bubble Sort)
시간 복잡도: O(n^2)
인접한 요소들을 비교하여 정렬하는 알고리즘으로, 반복문을 통해 정렬이 완료될 때까지 계속 비교 및 교환한다.
선택 정렬(Selection Sort)
시간 복잡도: O(n^2)
매번 최솟값을 찾아서 정렬되지 않은 부분의 첫 번째 요소와 교환하는 알고리즘이다.
삽입 정렬(Insertion Sort)
시간 복잡도: O(n^2)
정렬된 부분과 정렬되지 않은 부분을 나누고, 정렬되지 않은 부분의 요소를 적절한 위치에 삽입하여 정렬한다.
This post is licensed under CC BY 4.0 by the author.