삼각함수의 사인 법칙 증명
사인 법칙이 성립하는 이유
📌개요
사인 법칙이 모든 삼각형에서 어떻게 성립하는지 외접원을 이용한 증명을 정리
📌내용
사인 법칙 증명
모든 삼각형에는 외접원이 존재한다. $\triangle{ABC}$가 있고, 이 삼각형을 둘러싸는 외접원(circumcircle)을 고려하자. 외접원의 반지름을 R이라고 했을 때, 사인 법칙은 다음과 같이 성립한다.
\[\frac{a}{\sin{A}} = \frac{b}{\sin{B}} = \frac{c}{\sin{C}} = 2R\]- 여기서 $A,B,C$는 삼각형의 각(angle)
- $a,b,c$는 각각 그에 대응하는 변의 길이(length)
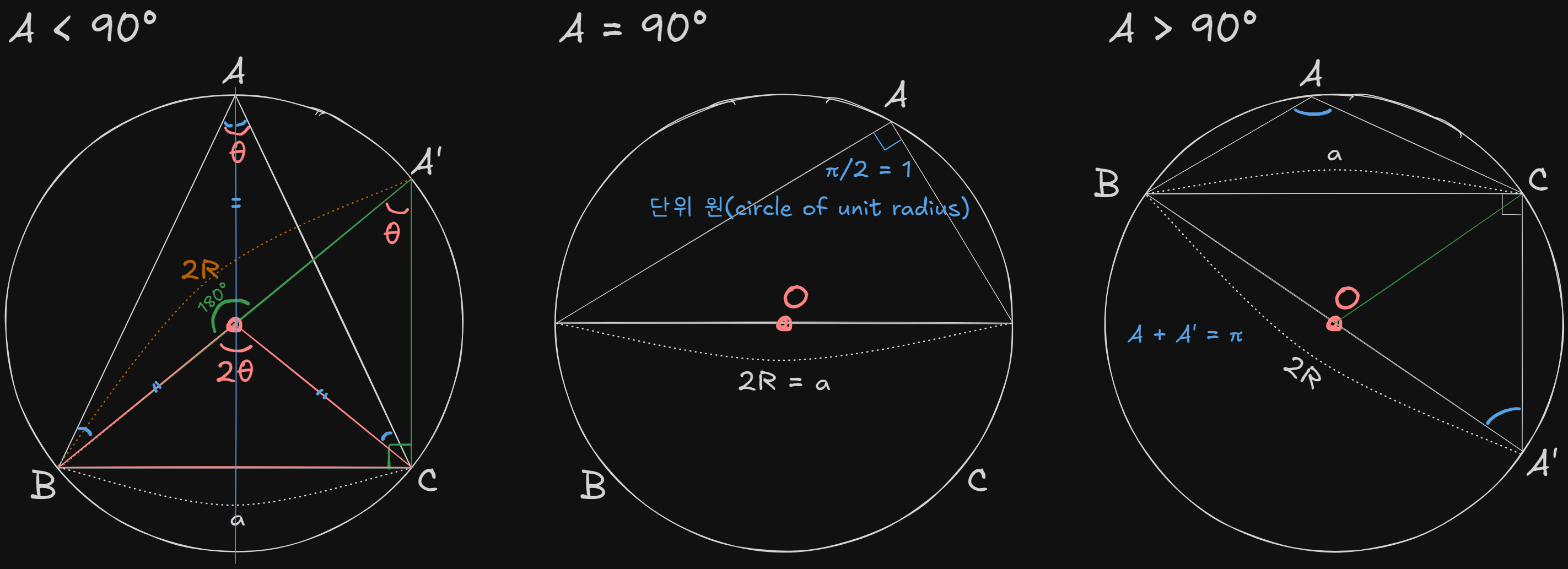
A < 90
$A$가 $\overparen{BC}$에 대한 원주각을 이루는 점이다. 외접원의 중심을 포함하며 $\overparen{BC}$에 대한 원주각이 동일하도록 $A’$을 설정하면, $\triangle{ABC}$의 외접원의 지름($2R$)을 빗변으로 갖는 $\triangle{A’BC}$을 확인할 수 있다.
\[\begin{gathered} \angle A = \angle A' \\ \sin A' = \frac{a}{2R} = \sin A \\ \therefore 2R = \frac{a}{\sin A} \end{gathered}\]같은 방식으로 $B$, $C$에 대해서도 확인할 수 있다.
A = 90
단위 원(circle of unit radius)
- $\sin{\theta}$ 는 각 $\theta$ 에 대한 y좌표
- $\cos{\theta}$ 는 각 $\theta$ 에 대한 x좌표
$\theta = \frac{\pi}{2}$(즉, $90^\circ$)일 때 좌표 확인, y축의 가장 위쪽에 해당하는 점
\[(\cos{\frac{\pi}{2}},\sin{\frac{\pi}{2}}) = (0,1)\]직각인 $A$를 이용해서 $\sin A$가 1임을 확인한다.
\[\sin{A} = \sin{90^\circ} = 1\]그 다음 반원에 대한 지름 $R$, 빗변 $a$를 이용해 확인한다.
\[\begin{gathered} a = 2R = 2R \times 1 = 2R \times \sin{A} \\ a = 2R \times \sin{A} \\ \therefore 2R = \frac{a}{\sin{A}} \end{gathered}\]같은 방식으로 $B$, $C$에 대해서도 확인할 수 있다.
A > 90
내접 사각형의 성질을 활용하여 마주보는 두 각의 합이 $\pi (180^\circ)$임을 이용한다.
$\triangle{ABC}$의 빗변인 $a = \overline {BC}$ 를 한 변으로 갖는 $\triangle{A’BC}$(직각삼각형)를 설정한다. 외접원에 내접하는 사각형 $ABA’C$의 성질을 이용한다.
\[\angle A + \angle A' = 180 ^\circ\]$A$, $A’$은 서로 다른 각이지만, 삼각함수의 성질에 의해 $A$, $A’$이 보완각 관계를 가지므로 사인 값이 동일하다. $\sin$ 함수는 원을 기준으로 y축 값을 측정하는 거라서, 비록 $A$와 $A’$이 다르게 생겼다고 해도 사인 값 자체는 동일하게 유지된다.
\[\begin{gathered} \sin{A'} = \frac{a}{2R} = \sin{(180 ^\circ - A)} = \sin{A} \\ \sin{A} = \frac{a}{2R} \\ \therefore 2R = \frac{a}{\sin{A}} \end{gathered}\]같은 방식으로 $B$, $C$에 대해서도 확인할 수 있다.
⚙️EndNote
보완각 성질의 본질
- 단위원(Unit Circle)을 생각하자.
- $\angle A$가 1사분면에 있을 때, 이를 2사분면으로 반사 시키면 $180^\circ - A$가 된다.
- 이때 삼각비의 정의에 따라 $\sin (180 ^\circ - A) = \sin A$ 왜냐하면, 단위원에서 y좌표는 그대로 유지되기 때문이다.